Вероятностные расчеты расстояния выстрела по диаметру рассеивания дроби
/ Лисицын А.Ф. // Судебно-медицинская экспертиза. — М., 1974 — №2. — С. 10-14.

УДК 340.624.4
PROBABILITY ESTIMATIONS OF DISTANCE OF SHOT: A FUNCTION OF THE DISPERSION OF PELLETS
A. F. Lisitzyn
Experimental data were studied statistically. An equation demonstrating the dependence between the diameter of the dispersion area of shot pellets and the distance of shot is presented.
Попытки определять дистанцию выстрела эмпирически по диаметру рассеивания дроби не дают желаемых результатов. Опыт показывает, что без математического анализа процесса рассеивания этот вопрос нельзя решить достаточно точно.
В настоящей работе поставлены задачи: 1) используя методы математической статистики, рассчитать с достаточно высокой вероятностью амплитуду случайных колебаний рассеивания дроби; 2) определить зависимость между диаметром рассеивания дроби и ее номером (размером); 3) исследовать характер зависимости между диаметром рассеивания и расстоянием выстрела, найти формулу, определяющую эту зависимость, и получить таким образом данные для практического определения дистанции выстрела по площади поражения.
Выстрелы производили из ружей 12, 16 и 20-го калибра с расстояния 5, 10, 15 и 20 м патронами с дробью от № 11 диаметром 1,5 мм до картечи диаметром 7 мм, снаряженными как бездымным, так и дымным порохом, сериями по 10, 30 и 100 патронов. Условия стрельбы в пределах одной серии не менялись. Мишенями служили листы плотной бумаги, прикрепленной к деревянному щиту. Площадь рассеивания дроби на мишенях измеряли линейкой в двух взаимно перпендикулярных направлениях, после чего вычисляли средний диаметр площади; (половина суммы двух измерений, округленная до целых чисел — сантиметров) .
Математически обработали результаты 670 экспериментов — 43 серии.
Результаты каждой серии выстрелов были представлены в виде вариационного ряда диаметров рассеивания дроби x1, x2...xn (xi+1).
Параметры вариационных рядов, т. е. среднее арифметическое значение — х и среднее квадратическое отклонение — σ вычисляли по общепринятым формулам:
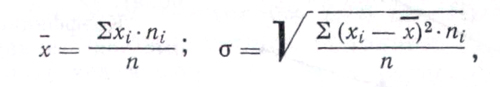
где xi — варианты диаметров рассеивания; ni—частоты вариантов; n — число опытов в серии.
Необходимо было вычислить для каждого вариационного ряда доверительные границы (крайние варианты рассеивания), которые охватывали бы практически все диаметры рассеивания дроби, возможные при определенных условиях стрельбы одной серией патронов. Чтобы выполнить такие вычисления, требовалось сначала найти закон, которому подчиняется рассеивание дроби в статистическом отношении. Характер эмпирического распределения диаметров рассеивания позволил предположить, что экспериментальные данные подчиняются теоретическому распределению Роллея. Проверка этой гипотезы производилась с помощью двух известных критериев: «хи-квадрат» (К. Пирсон) и А.Н. Колмогорова. Оба метода, примененные к нескольким вариационным рядам, показали, что предложенная гипотеза не противоречит опытным данным и может быть принята с вероятностью Р>50%.
Для расчета доверительных границ рассеивания использовалась интегральная функция распределения Релея, задающая вероятность того, что случайный радиус X не превзойдет некоторого числа х:
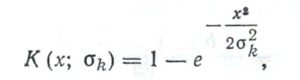
где К — интегральная функция; е — основание натуральных логарифмов; σk — радиальное среднее квадратическое отклонение, вычисляемое по формуле σk=σ/0,655; х — диаметры рассеивания дроби. В данном случае представляли интерес два значения х: минимальное, которое нами обозначено как x1, и максимальное — x2.
Из приведенного уравнения при заданной вероятности исследуемого интервала Р = 99,9% путем элементарных математических выкладок были выведены формулы для расчета доверительных границ рассеивания дроби в рядах распределения.
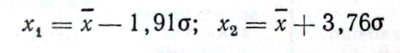
(x1 и x2 — доверительные границы; х — средний диаметр для данного ряда; σ — среднее квадратическое отклонение.
После вычисления по этим формулам доверительных границ рассеивания дроби для всех вариационных рядов исследовали зависимость между величиной рассеивания и диаметром дроби путем построения и анализа графиков.
Для каждого расстояния выстрелов составляли отдельный график. Расположение точек на графиках указывало на линейную зависимость диаметров рассеивания дроби от ее номера (размера) и в то же время свидетельствовала о случайном варьировании полученных диаметров, поскольку для вычисления их использовали экспериментальные параметры вариационных рядов. Чтобы выявить основную тенденцию зависимости, производили выравнивание (сглаживание) рядов точек по методу наименьших квадратов, для чего использовали линейное уравнение: у=a0+a1x, в котором х — номер дроби; у — диаметр ее рассеивания. Сущность метода заключается в нахождении таких коэффициентов уравнивания, при которых сумма квадратов отклонений исходных значений у от теоретических (вычисленных по данному уравнению) окажется наименьшей (В.Ю. Урбах, 1963). Эти расчеты ввиду их (громоздкости не приводятся. Таким способом рассчитали линии регрессии у по х для минимальных и максимальных диаметров рассеивания дроби при расстоянии выстрелов 5, 10 и 20 м и по уравнениям регрессии вычислили теоретическое значение диаметров рассеивания для всех номеров дроби, в том числе для тех, с которыми экспериментов не проводили.
Ко всем линиям регрессии определяли также коридоры ошибок по изложенной ранее методике (В.П. Спиридонов и А.А. Лопаткин, 1970).
Результаты проведенных расчетов позволили исследовать зависимость между диаметром рассеивания дроби и расстоянием выстрела. Известно, что эта зависимость нелинейна и графически выражается пологой восходящей кривой. Поэтому исчисленные описанными выше способами диаметры рассеивания дроби разных номеров вторично выравнивались квадратичной функцией вида у=a0+a1x+a2x2, где х — расстояние выстрела; у — диаметры рассеивания дроби (см. рисунок). Коэффициент a0 в указанном уравнении (равный диаметру канала ствола) был заменен постоянным средним числом 1,6 (для ружей 12, 16 и 20-го калибра). Коэффициенты а1 и а2 вычисляли с помощью системы нормальных уравнений (В.Ю. Урбах, 1963). Однако для того, чтобы выполнить эти расчеты для всех номеров дроби и для различных условий стрельбы, пришлось бы решать систему уравнений более 80 раз. Поэтому расчет коэффициентов квадратного уравнения по исходным данным был произведен на ЭВМ по специальной программе, составленной в вычислительном центре (Л. Н. Иванова).
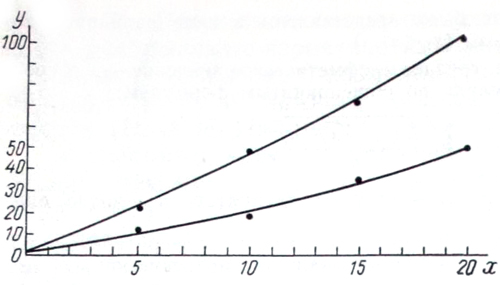
Кривые уравнения у=a0+a1x+a2x2, отражающие зависимость минимальной и максимальной границ рассеивания дроби от расстояния выстрела.
По оси абсцисс — расстояния выстрелов (в м): по оси ординат — диаметры рассеивания дроби (в см).
Коэффициенты a1 и a2 исчисленные для стандартных условий стрельбы и для условий, вызывающих повышенное рассеивание, представлены в табл. 1. Под стандартными условиями следует понимать применение нормальных охотничьих ружей и снаряженных по правилам патронов, в том числе и фабричных. Рассеивание увеличивается при дымном порохе, укороченных гильзах, разделении дроби прокладками, при стрельбе из стволов с дульными расширениями или из обрезов, а также при некруглой дроби, самодельных пыжах и т. д.
Пользуясь таблицей коэффициентов и зная номер дроби, а также особенности патронов и оружия, можно рассчитать по диаметру рассеивания искомые пределы расстояния выстрела. Известно, что корни квадратного уравнения 0= с+bx+ах2 определяются по формуле:
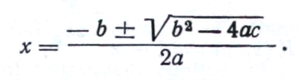
Применяя это правило к уравнению y=a0+a1x+a2x2, получим 0=(а0—у)+a1x+а2х2, откуда
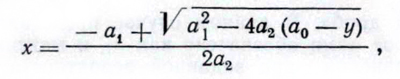
где х — расстояние выстрела; у — диаметр рассеивания дроби; а0, а1, а2 — коэффициенты уравнения.
Таблица 1
Исчисленные на ЭВМ коэффициенты уравнения у = а0 +a1x+а2х2, определяющие величину рассеивания дроби (а0 + 1,6)
|
№ дроби |
Диаметр дроби (в мм) |
Для стандартных условий | Для увеличенного рассеивания | ||||||
|
минимум |
максимум |
минимум |
максимум | ||||||
|
а1 |
а2 |
а1 |
а2 |
а1 |
а2 |
а1 |
а2 | ||
|
9 |
2 |
1,38 |
0,062 |
4,31 |
0,058 |
2,23 |
0,086 |
6,63 |
0,081 |
|
8 |
2,25 |
1,33 |
0,061 |
4,23 |
0,056 |
2,16 |
0,085 |
6,52 |
0,077 |
|
7 |
2,5 |
1,30 |
0,059 |
4,17 |
0,052 |
2,11 |
0,082 |
6,42 |
0,072 |
|
6 |
2,75 |
1,25 |
0,058 |
4,07 |
0,051 |
2,03 |
0,081 |
6,27 |
0,070 |
|
5 |
3 |
1,20 |
0,057 |
4,00 |
0,048 |
1,97 |
0,079 |
6,16 |
0,065 |
|
4 |
3,25 |
1,15 |
0,056 |
3,93 |
0,044 |
1,90 |
0,077 |
6,04 |
0,062 |
|
3 |
3,5 |
1,11 |
0,055 |
3,85 |
0,042 |
1,85 |
0,076 |
5,94 |
0,056 |
|
2 |
3,75 |
1,07 |
0,053 |
3,79 |
0,038 |
1,78 |
0,076 |
5,85 |
0,050 |
|
1 |
4 |
1,03 |
0,052 |
3,72 |
0,035 |
1,70 |
0,072 |
5,73 |
0,047 |
|
0 |
4,25 |
0,98 |
0,051 |
3,64 |
0,032 |
1,63 |
0,070 |
5,62 |
0,042 |
|
00 |
4,5 |
0,94 |
0,049 |
3,57 |
0,029 |
1,58 |
0,067 |
5,52 |
0,037 |
|
000 |
4,75 |
0,89 |
0,048 |
3,50 |
0,026 |
1,52 |
0,065 |
5,41 |
0,033 |
|
0000 |
5 |
0,84 |
0,047 |
3,42 |
0,024 |
1,43 |
0,064 |
5,28 |
0,029 |
|
к |
5,25 |
0,80 |
0,046 |
3,34 |
0,021 |
1,36 |
0,063 |
5,18 |
0,024 |
|
к |
5,5 |
0,76 |
0,044 |
3,27 |
0,018 |
1,30 |
0,061 |
5,07 |
0,020 |
|
к |
5,75 |
0,71 |
0,044 |
3,20 |
0,014 |
1,23 |
0,059 |
4,96 |
0,015 |
|
к |
6 |
0,67 |
0,042 |
3,12 |
0,012 |
1,17 |
0,057 |
4,85 |
0,011 |
|
к |
6,5 |
0,60 |
0,039 |
2,98 |
0,006 |
1,07 |
0,052 |
4,57 |
0,006 |
|
к |
7 |
0,49 |
0,037 |
2,75 |
0,006 |
0,92 |
0,049 |
4,20 |
0,004 |
|
к |
7,5 |
0,40 |
0,035 |
2,55 |
0,004 |
0,76 |
0,046 |
3,80 |
0,003 |
|
к |
8 |
0,30 |
0,033 |
2,30 |
0,003 |
0,63 |
0,043 |
3,50 |
0,002 |
|
к |
8,5 |
0,29 |
0,027 |
2,00 |
0,002 |
0,63 |
0,032 |
3,20 |
0,001 |
Пример расчета. Размеры площади поражения 28×32 см. Тогда средний диаметр (у) равен (28+32)/2 =30 см. Дробины соответствуют по размеру (весу) дроби № 6 диаметром 2,75 см. Выстрел производился бездымным порохом при стандартных условиях. Для вычисления предельных дистанций выстрела подставим в формулу (1) числовые значения коэффициентов и диаметр рассеивания дроби. Коэффициент а0 равен 1,6 (постоянное число), коэффициенты а1 и а2 для дроби № 6 при стандартных условиях стрельбы найдем по табл. 1. При минимальном рассеивании: а1=1,25; а2=0,058. При максимальном рассеивании: а1=4,07; а2=0,051. По коэффициентам минимального рассеивания определим дальнюю границу расстояния выстрела:

Ближнюю границу дистанции вычислим по коэффициентам максимального рассеивания:

Следовательно, искомое расстояние выстрела находится в границах от 6.5 до 13,8 м. То есть диаметр рассеивания 30 см при данных условиях может быть только в пределах этой дистанции (с вероятностью 99,9%).
Таблица 2
Максимальные ошибки при расчетах расстояния выстрела (при доверительной вероятности 99%)
| Ближняя граница | Дальняя граница | ||
| исчисленное расстояние выстрела (в м) | ошибка (в м) | исчисленное расстояние выстрела (в м) | ошибка (в м) |
| 0,5—1 | ±0,08 | 1—2,5 | ±0,4 |
| 1—2 | ±0,2 | 2,5—5,5 | ±0,8 |
| 2—4,5 | ±0,4 | 5,5—10 | ±1,1 |
| 4,5—6,5 | ±0,7 | 10—15 | ±1,5 |
| 6,5—8,5 | + 1 | 15—20 | ±1,7 |
| 8,5—10,5 | ±1,1 | 20—30 | ±2 |
| 10,5—12,5 | ±1,4 | 40—50 | ±2,4 |
| 12,5—20 | ±2,3 | Далее 50 | ±3 |
| 30-40 | ±5 | — | — |
| Далее 50 | ±8 | ||
Каждый предел расстояния вычисляется с определенной статистической ошибкой, которую можно найти по табл. 2. Ошибки вычислены с доверительной вероятностью 99%.
Применение табл. 2 не требует дополнительных расчетов. Так, в нашем примере, где установлено расстояние выстрела от 6,5 до 13,8 м, ошибка ближней границы составит ±0,7 м, а дальней ±1,5 м.
Описанный расчет применим и к нахождению близких дистанций выстрела (до 2 м), но при соблюдении следующих условий:
- В качестве коэффициента а0 необходимо подставлять точное значение диаметра канала ствола у дульного среза.
- Исчисленные пределы расстояния выстрела следует увеличивать на 20%, если в патроне применялись средства, уменьшающие рассеивание дроби, например полиэтиленовый пыж-контейнер.
Таблицу коэффициентов, по которой вычисляются предельные расстояния выстрела, можно использовать для ружей разных калибров и с различной сверловкой.
Выводы
- Диаметры рассеивания дроби являются вариантами случайной величины, которая подчиняется теоретическому распределению Релея. На основании этого закона в любой однородной совокупности диаметров рассеивания дроби, образующих вариационный ряд, можно вычислить доверительные границы, в пределах которых будет находиться не менее 99,9% всех диаметров рассеивания, возможных при данных условиях.
- Предложена методика вычисления коэффициентов квадратного уравнения определяющих величину рассеивания дроби при разных условиях стрельбы. Эти данные можно рекомендовать для практических расчетов дистанции выстрела.
похожие статьи
Возможность определения расстояния выстрела из охотничьего оружия 12-го калибра по признакам повреждений одежды и соответствующим им математическим моделям / Суворов А.С., Белавин А.В., Макаров И.Ю., Страгис В.Б., Райзберг С.А., Гюльмамедова Н.Д. // Судебно-медицинская экспертиза. — М., 2019. — №2. — С. 19-21.
Установление расстояния выстрела из охотничьего оружия 12-го калибра патронами с пыжом-контейнером по особенностям входных повреждений на одежде / Суворов А.С., Белавин А.В., Макаров И.Ю., Зеленский С.А., Страгис В.Б., Райзберг С.А. // Судебно-медицинская экспертиза. — М., 2019. — №1. — С. 8-12.
Признаки дробовых повреждений из газового стволового оружия / Кузнецов Ю.Д., Бабаханян Р.В., Исаков В.Д. // Матер. IV Всеросс. съезда судебных медиков: тезисы докладов. — Владимир, 1996. — №1. — С. 70-71.
Особенности дробового ранения груди выстрелом из сигнального пистолета Шпагина, переделанного для стрельбы охотничьими патронами / Гусаров А.А., Макаров И.Ю., Фетисов В.А., Суворов А.С. // Вестник судебной медицины. — Новосибирск, 2017. — №4. — С. 59-63.
Возможности экспертной оценки влияния конструктивных особенностей ствола охотничьего оружия на признаки повреждений, формируемых выстрелами многоэлементным снарядом в цилиндрическом контейнере / Макаров И.Ю., Суворов А.С., Лоренц А.С. // Судебно-медицинская экспертиза. — М., 2016. — №6. — С. 22-26.