Моделирование падения на плоскость в результате толчка

Важная роль в заключении эксперта отводится исследованиям с использованием методов точных фундаментальных наук (математики, физики), что применяется в современных исследованиях судебных медиков по изучению биомеханик и движения тела человека [Громов А.П., 1979; Пашинян Г.А., Ромодановский П.О., Беляева Е.В., 1999; Ромодановский О.А., Щербин Л.А., Савостин Г.А., Дербоглав В.В., 1972].

Для изучения травмы падения тела человека после толчка на жесткую поверхность нами построена математическая модель динамики движения объекта (тело человека в позиции стоя прямо), которая рассматривает движение человека, опрокидывающегося навзничь с последующим продвижением по плоскости. В данной модели объект рассматривается как неоднородный стержень, который вращается вокруг оси, где роль шарнира выполняет пяточный сустав.

Толчковое воздействие со стороны нападающего на пострадавшего (объект) моделируется силой Ft, приложенной на расстоянии ht от горизонтальной поверхности и на протяжении времени при повороте тела на угол φ (рис. 1).

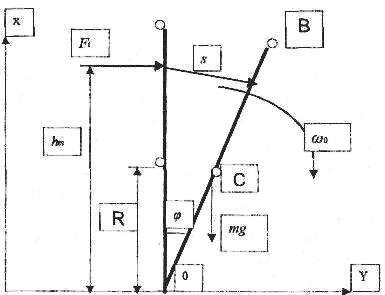
Рис. 1. Схематичное изображение выведения из равновесия объекта в результате воздействия силы Ft

Угол поворота φ определяется как функция от расстояния S, которое равно длине выдвижения руки с наклоном туловища толкающего.

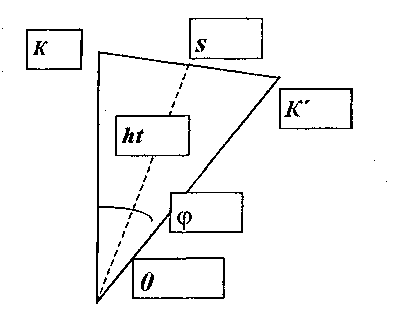
S - путь разгона тела (м), т.е. перемещение тела при толчке. Величина S является варьируемым параметром, зависимым от длины выдвигаемой руки с наклоном туловища толкающего: 0,05 < S < 1,0. В процессе моделирования S меняет свое значение в определенных допустимых значениях Smin<S<Smax определяется выдвижением руки нападающего и анатомическими её размерами. Не трудно получить зависимость угла поворота тела до выведения из равновесия φ от расстояния разгона тела S. Действительно, из равнобедренного треугольника OKK` (рис. 2) следует:

S/2 = ht sinφ / 2, т.е. φ = 2 arcsin (S/2ht) рад.

Алгоритм определения основных величин рассматриваемого процессавыстраивается из следующих вычислительных действий:

1. Считая ускорение at - постоянным, получим

at = 2St / τt² (м/сек²);

где at - ускорение толчка (считается постоянным), то есть Ft const; St - силовой имnульс (Н/с); τt - время толчка (с). По теории бокса τt>0,03 с [Дегтярев ИЛ., 1979];

2. В первом приближении толкающая сила Ft = const (Н) равна:

Ft = М * at = р М at = 2рМS/ τt²;

где М* ? р М - масса толкания (кг) (р -доля перераспределения массы при толчке и определяется экспериментально, варьируется при математическом моделировании: 0,3 < р <0,9); М - масса толкающего тела (кг);

Эта сила задает относительно точки О момент силы:

тО (Ft) = Ftht;

где ht =0,851 - расстояние (м) от горизонтальной поверхности по линии действия до горизонтально толкающего импульса St (Н *с);

3. Определение угловой скорости, приобретаемой телом в конце толчка. Из теоремы об изменении кинетической энергии механической системы [Бутенин Н.В., Лунц Я.Л., Маркин Д.Р., 1985; Леви-Чивита Т., Амальди Ч., 1951] следует:

1/2 JO ω0² = Ftht + mght(1-cos φ),

где JO - момент инерции относительно подошвенной поверхности; ω0 - угловая скорость, приобретаемая телом в конце толчка; φ - угол поворота тела вокруг точки 0 до выведения из равновесия (зависит от величины перемещения тела при толчке s); m - масса тела (кг) ; 1 - длина тела (м); g - ускорение свободного падения (м/c²).

Отсюда вытекает формула значения угловой скорост и ω0 в конце толчка:

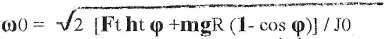(1)

- расстояние от стоп до центра масс (м).

Таким образом, в результате толчка тело приобретает угловую скорость ω0

4. Фаза падения тела на пол:

рассматриваем два положения тела: в первое мгновение пос­ ле толчка и в момен т соприкосновени я с поверхностью. Тогда имеет место теория об изменении кинетической энергии:

1/2 JO ω1² -1/2 JO ω0² = mgR (cos φ - sin α),

где

• ω1 - конечная угловая скорость пр и соударении о поверхность (с -1 ) ;
• а = 7,5° - угол устойчивост и [Пашинян Г.А., Ромодановский П.О., Беляева Е.В., 1999; Ромодановский О.А., Щерби н Л.А., Савос- тинГ.А., Дербогла в В.В., 1972];
• φ - угол поворота тела пр и толчке.

Следовательно, угловая скорость тела в момент удара о поверхность будет равна:

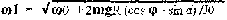
Далее повторяются формулы расчета перемещения тела во всех остальных фазах движения.

Фаза подбрасывания тела при ударе о плоскость. Фаза скольжения тела по плоскости.

Применяя теорему об изменении кинетического момента, получим выражения угловой скорости:

ω0 = Ft ht τt / JO,

Подставляя значение силы Ft, получим выражение угловой скорости:

ω0 = 2p M S ht τt / JO,

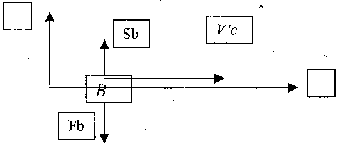
Величина силы толчка зависит от величины толкающей массы М*, ускорени я толчка at. Сила толчка прямо пропорционально увеличивает угловую скорость, приобретаемую телом в конце толчка. В свою очередь ω0 влияет на конечную угловую скорость ω1 на момент соударения о наклонную поверхность и ударный импульс в результате контакта головы (В) с поверхностью Sb и силу соударения головой о горизонтальную поверхность Fb. Ударный импульс после контакта головы с поверхностью напрямую влияет на время отскока (Г ) от поверхности после первичного удара и составляющую скоростей относительно продвижения оси X по горизонтальной поверхности (v"cx). И как итог возможен расчет расстояния (d) продвижения центра тяжести тела (С) по поверхности.

Сила соударения головой о горизонтальную поверхность Fb (рис.3) может быть рассчитана по формуле:

Fb = Sb / tb

Где

• Fb - сила соударения головой о горизонтальную поверхность (Н);
• Sb - ударный импульс в результате контакта головы с поверхностью (Нос);
• tb - время удара головы о поверхность (с).

По литературным данным, время удара головы о жесткую поверхность составляет 0,006-0,007с, о полужесткую поверхность - 0,007-0,009с, о нежесткую поверхность - 0,021-0,030с [Громов А.П., 1979].

Рис. 3. Схематическое изображение соударение головы (В) о жесткую поверхность и продвижения по оси X.

d = V`cx τcb + d<sub>c</sub> = V`cx τcb + 1/2 V`cx / ( fT g ),

где

• τcb - время нахождения тела в свободном падении
• dc - путь, пройденный центром тяжести в скольжении (d_c = 1/2 V`cx / ( fT g ))
• V`cx - скорость продвижения тела после удара по оси X,
• fT - коэффициент трения, скольжения тела по поверхности.

Кинематика движения тела при толчке в грудь имеет характерные признаки: более длительное время взаимодействия между контактирующим и телами τt на определенной дистанции "разгона" S, высокая масса толкающего тела рМ.

Названные факторы определяют более значительное перемещение тела пострадавшего на расстояние d после толчка. В практике бокса резкий удар [Дегтярев И.П., 1979] не влечет за собой отбрасывания тела противника. При снижении резкости удара (удар превращается в толчок) на противника действует большая масса толкающего тела рМ, что приводит к отбрасыванию на более значительное расстояние d.

Для решения вопроса о силе соударения головой Fb о поверхность при свободном падении и определения расстояния продвижения тела по плоскости необходимо определить величины параметров: величину ударного импульса Sb (результат контакта головы с поверхностью), коэффициент трения тела fT при скольжени и по поверхности и так далее. Эти задачи могут быть решены путем экспериментальных наблюдений и сопоставления полученных результатов с физико-математической моделью и литературными данными.