Математическое моделирование падения с высоты роста после удара
/ Авдеев А.И., Лейбович М.В. // Избранные вопросы судебно-медицинской экспертизы. — Хабаровск, 2000 — №3. — С. 22-27.

Кафедра судебной медицины ДВГМУ, г. Хабаровск (зав. - доц. А.И. Авдеев)
Кафедра теоретической механики ХГТУ, г. Хабаровск (зав. - доц М.В. Лейбович)
Научные исследования, представляющие различные школы судебных медиков, для решения актуальных вопросов судебно-медицинской травматологии, биомеханик и травмы опираются на точные науки [Гедыгушев И.А., 1999; Громов А.П., 1979; Крюков В.Н., 1995; Пашинян Г.А., Ромодановский П.О., Беляева Е.В., 1999; Ромодановский О.А., Щербин Л.А., Савостин Г.А., Дербоглав В.В.,1972]. При изучении процесса падения была предложена модель, при которой биоманекен был закреплен в раме на специальном стенде [Громов А.П., 1979], что не позволяло определить реакции опоры при свободном положении тела и продвижение его по плоскости после падения.
При изучении травмы падения тела человека на жесткую поверхность нами поставлены следующие задачи:
- сформулировать математическую модель динамик и движения объекта (в нашем случае тела человека в положении стоя прямо);
- получить расчетные формулы по определению кинематических и силовых характеристик движения в его различных фазах;
- по результатам численного расчета провести анализ картины происшествия определить вероятностные причины падения объекта с реконструкцией обстоятельств причинения повреждений.
Построенная математическая модель рассматривает движение человека, опрокидывающегося навзничь. При этом человек рассматривается как неоднородное тело неизменяемой структуры (не учитывается переменность расположения центра масс, момент инерции, многостепенная свобод а относительных перемещений сегментов тела). В представленной модели объект рассматривается как стержень, способный вращаться вокруг оси. Роль шарнира выполняет пяточный сустав. Поверхность, на которой находится тело, представляет собой не удерживающуюся, стационарную связь, характеризуемую коэффициентами трения, скольжения и восстановления при упругом ударе.
Основой математической модели движения рассматриваемого объект а (тела человека в положении стоя прямо) являются методы теоретической механики, в частности, динамика механической системы и теории удара [Леви-Чивита Т., Амальди Ч., 1951 ; Бутенин Н.В., Лун ц Я.Л., Марки н Д.Р., 1985]. В расчетах по определению перемещения и сил применяется метод варьирования исходных параметров модели.
Самопроизвольное падение (навзничь) происходит при выведении объекта из равновесия. В последних публикациях по биомеханике травмы [Пашинян Г.А., Ромодановский П.О., Беляева Е.В., 1999] анализируется случай падения тела человека навзничь, в результате которого устанавливается значение внешней силы, затраченной на опрокидывание тела. При этом строится физико-математическая модель поведения тела человека после выведения его из состояния устойчивого равновесия с учетом и без учета силового импульса (то с учетом начальной угловой скорости ω0 > 0 или ω0 = 0). Так согласно теореме об изменении кинетической энергии (в случае начальной угловой скорости ω0 = 0), значение угловой скорости тела ω в момент соприкосновения с горизонтальной поверхностью определяется по формуле: Варьируемыми параметрами являются масса m и длина 1 объекта. В конкретном случае эт и параметры определяются экспериментально и считаются исходным и и известными величинами. Согласно вышеприведенным исходным параметрам имеем расчетную формулу угловой скорости в момент удара о горизонтальную поверхность: где (c-1) - радиан-секунда, размерность угловой скорости. Рассмотрим случай движения тела при действии горизонтального ударного импульса Su в голову. Расстояние от горизонтальной поверхности до центра тяжести головы обозначим h. По данным судебно-медицинской литературы следует, что h = 0,9411 (м) [Громов А. П., 1979]. Применяя основные уравнения динамик и при ударе, получим значение начальной угловой скорости вращения тела: J0 - момент инерции тела относительно оси вращения, проходящего через пятки. В зависимости от величины (а также и от направления) ударного импульса (удара) будут происходить различные перемещения тела. Так при горизонтальном ударе, если ударный импульс Su удовлетворять неравенству: где fm - коэффициент трения, скольжения,
τu - время удара, тогда точка 0 в послеударный период начнет перемещаться, а тело падает с угловой скоростью
ω. То есть, тело будет совершать плоско параллельное движение. На основании выше приведенных исходных данных получим неравенство: Su > 30,31 fmτu . При условии для
τu=0,018 с, m=70 кг, имеем Su = 38,2 f. При f >0,2 и при скорости
движения руки ударяющего v < 10 м/с, что сопоставимо с аналогичным и параметрами удара в боксе [Дегтярева И.П., 1979], не происходит перемещения (скольжения и отрыва) точки опоры
ног с горизонтальной поверхности. Поэтому дальнейшее движение есть вращение вокруг точки 0. Угловая скорость ω, с которой тело упадет на горизонтальную поверхность, будет равна: Из-за незначительной величины ударного импульса Su угловая скорость ω практически одинакова для
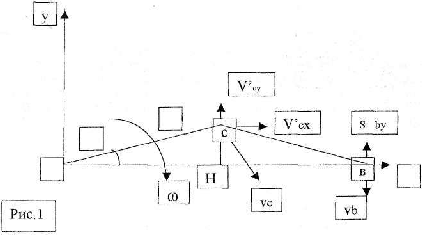
3 < v < 10 м/с. Следующей фазой динамического процесса является удар тела о горизонтальную поверхность (рис.1) Введем обозначения: Vc скорость центра масс (точка С), Vb скорость точек контакта головы с поверхностью (точка - В), ω - угловая скорость до удара; V`c, V`b, ω" - скорость после удара. Согласно кинематике вращательного движения: Vc = ωR; , Vb = ωOB; где OB = h cos α. Предполагается, что удар тела приходится на голову, то соотношение проекций скоростей точки В на ось У определяется формулой: V`by = -kVb , где k - коэффициент восстановления при упругом ударе. По данным специальной литературы [Громов А.П., 1979], при соударении головой (для различных поверхностей) имеются следующие значение этого коэффициента: Составляя уравнения динамик и тела при ударе в проекция х на оси, получим: Вводя гипотезу Раусса [Леви-Чивита Т., Амальд и Ч., 1951] о соотношениях проекций ударного импульса, будем иметь дополнительные уравнения: Совместно решая систем у уравнений (3), (4) получим: Где Варьируя значения скорости удара при заданных массах ударяющего и ударяемого, получим набор значений кинематических параметров тела после удара Получив при ударе начальные кинематические характеристики Не учитывая вертикальную составляющую скорости центра масс тела, можно определить горизонтальную составляющую скорости при "приземлении " на поверхность после отскока, которая и будет являться начальной скоростью при скольжении тела на горизонтальной поверхности. Обозначая через Тогда путь, пройденный центром тяжести в скольжении, будет равен: Полный путь, пройденный центром тяжести за весь цикл движения, равен: Расчёты показывают, что это расстояние незначительно отличается для различных значений скорости ударяемой массы v. Таким образом, физико-математическая модель процесса удара позволяет проследить особенности внешнего воздействия на рассматриваемое тело и реакцию опоры при падении, определить в перспективе параметры, позволяющие установить взаимосвязь между величиной силового импульса (силой травматического воздействия) и силой соударения о плоскость и перемещением тела потерпевшего на плоскости.

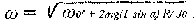
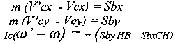 (3)
(3)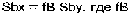 - коэффициент трения, скольжения головы по поверхности. Заключающее уравнение составляется на основе формулы Эйлера для скоростей точек тела при плоском движении [Бутенин Н.В., Лунц Я.Л., Маркин Д.Р., 1985]. Это уравнение в проекции на ось У запишется:
- коэффициент трения, скольжения головы по поверхности. Заключающее уравнение составляется на основе формулы Эйлера для скоростей точек тела при плоском движении [Бутенин Н.В., Лунц Я.Л., Маркин Д.Р., 1985]. Это уравнение в проекции на ось У запишется: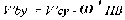 (4)
(4) (5)
(5)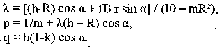
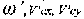 , а также значения ударного импульса. Как и следовало ожидать, полученные значения практически не отличаются при изменении скорости удара от 3 до 10 м/с.
, а также значения ударного импульса. Как и следовало ожидать, полученные значения практически не отличаются при изменении скорости удара от 3 до 10 м/с.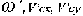 можно рассчитать дальнейшее движение тела. Так из дифференциальных уравнений плоского движения нетрудно получить закон перемещения тела:
можно рассчитать дальнейшее движение тела. Так из дифференциальных уравнений плоского движения нетрудно получить закон перемещения тела: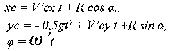 (б)
(б)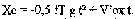
![]() - коэффициент трения, скольжения тела по поверхности (следует отметить, что
- коэффициент трения, скольжения тела по поверхности (следует отметить, что  ), запишем закон скольжения тела по горизонтальной поверхности:
), запишем закон скольжения тела по горизонтальной поверхности: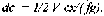
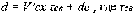 - время нахождения тела в свободном падении.
- время нахождения тела в свободном падении.
похожие статьи
Повреждения, возникающие при падении на плоскость / Шпехт Д.Ю., Туркевич И.Я. // Мат. VI Всеросс. съезда судебных медиков. — М.-Тюмень, 2005. — №. — С. .