Моделирование падения тела человека на наклонную поверхность

При падении, в упрощенном представлении, тело человека представляет несколько подвижных друг относительно друга частей, соединенных суставами, и обладающими определенными биомеханическими и физическим и характеристиками. Описание движения такой модели предполагает сложную систему нелинейных неоднородных дифференциальных уравнений второго порядка, устанавливающих зависимость между кинематическим и характеристиками движущегося тела, действующими силами и моментами мышечной тяги. В некоторых публикациях приводятся математические расчеты для установления силы соударения, угловой скорости и других параметров, характеризующих процесс перемещения тела человека, скорости и силы воздействия на тело после падения с высоты [Богданов В.А., Прудковский Б.А., Воронов В.А., 1972; Лебедев А.Н., 1986], падения на плоскости [Громов А.П., 1979; Пашинян Г.А., Ромодановский О.А., Беляева Е.В., 1999; Ромодановский О.А., Щербин Л.А., Савостин Г.А., Дербоглав В.В., 1972]. В нашей модели объект рассматривается как неоднородный стержень, способный вращаться вокруг оси; роль шарнира выполняет пяточный сустав. При этом поверхность представляет собой неудерживающуюся, стационарную связь, характеризуемую коэффициентами трения, скольжения и восстановления при упругом ударе.

При падении тела человека навзничь после удара основой математической модели движения рассматриваемого объекта (тела человека в положении стоя прямо) являются методы теоретической механики, в частности, динамика механической системы и теории удара [Бутенин Н.В., Лунц Я.Л., Маркин Д.Р., 1986; Гернет М.М., 1973; Леви-Чивита Т., Амальди Ч., 1951 ; Некрасов А.И., 1950].

Для решения этих вопросов нам и построена модель со следующим и параметрами:

1. Тело — неоднородный стержень со следующим и характеристиками:

l₀ — момент инерции относительно ног; m — масса тела ; l — длина тела ; R_c = 0,594 l — расстояние от точки 0 до центра масс тела С .

2. Место происшествия — поверхности соприкосновения с телом (рис.2): наклонная поверхность (пандус или лестничный марш) под углом d; горизонтальная плоскость; перила (поручни); стены, как ограничивающая боковое перемещение плоскость.

Процесс движения распределяется на следующие отрезки: падение тела на наклонную поверхность навзничь; скольжение по этой наклонной поверхности; скольжение по горизонтальной поверхности до остановки.

• В результате вращение вокруг точки 0 тело приобретает конечную угловую скорость φ падения о плоскость, а также скорость начала скольжений обозначим V₀ — горизонтальная составляющая начала скольжений тела по наклонной поверхности.
• Скольжение по наклонной плоскости имеет параметры движения: — коэффициент скольжения тела по плоскости (является заданной величиной); S₁ — расстояние, пройденное телом по наклонной плоскости до горизонтального участка; V₁ — скорость в момент перехода тела на горизонтальный участок траектории (эту величину требуется определить).
• Скольжение по горизонтальной поверхности: S2 — «тормозной путь», расстояние до остановки тела; ƒ_тр — если горизонтальная и наклонная плоскость выполнена из одного и того же материала, то ƒ_тр одинаков, в противном случае — разный (ƒ_тр1 , ƒ_тр2).

Движение по наклонной поверхности:

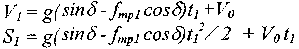(4)

где t₁ — время движения на 1-ом участке (по наклонной плоскости); V0 - скорость начала перемещения тела на наклонной плоскости.

t₁ = (V₁ - V₀) /а₁ → 2а₁S₁ =  (V₁ - V₀)² + 2V₀(V₁ - V₀);

V₀ — скорость, необходимая для преодоления расстояния S₂.

(6)

Замечание: Vo высчитывается по формуле (6) и является минимально возможной, так как не учитывается деформация тела, упругие свойства его отдельных частей, удары о поверхность и подскоки тела. Коэффициент трения ƒ_тр расчитываем экспериментально для каждого сочетания «материал - поверхность » из формулы. При равномерном движении

ƒ_тр = F_тр / mg

 Определение скорости тела V₀ при самопроизвольном падении тела. Так как Ппри самопроизвольном (пассивном) падении не учитывается ни толчок, ни ударный импульс, то имеем следующую зависимость :

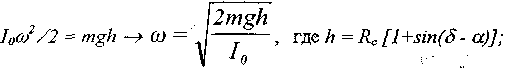
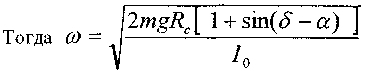
Расстояние от центра масс до уровня подошвенной поверхности R_c=0,594  l. Момент инерции тела относительно оси, проходящей в области пято к 1 = 0,4218 ml². Угол устойчивости а = 7,5° [Пашинян Г.А., Ромодановский О.А., Беляева Е.В., 1999 ; Ромодановский О.А., Щербин Л.А., Савостин Г.А., Дербоглав В.В., 1972]. Наклон поверхности типового лестничного марша под углом о" = 30°. В таком случае:

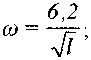
Для тела длиной l =1,7 скорость продвижения V_g по наклонной поверхности при пассивном (самопроизвольном ) падении будет определяться по формуле:

V₀ = ωR_c sin α = 4,74 * 0,594 l sin 7,5 = 0,624 м/с

Расстояние продвижения по горизонтальной поверхности S₂:

S₂ = S V_t² / gƒ_mp2

Согласно законам теоретической механики "предельная сила сцепления для случая скольжения не зависит при данной силе нормальной реакции от размера трущихся поверхностей". [Некрасов А.И., I960]. Коэффициенты трения скольжения не зависят ни от давления, ни от величины трущихся поверхностей, ни от скоростей. Они зависят от физической природы трущихся тел, от шлифовки поверхностей, от расположения волокон и конечно от смазки [Гернет М.М., 1973]. Исходя из кулоновских законов, скольжение стержня без ударов по выступающим гребням ступеням лестничного марша будет соответствовать скольжению по однородной наклонной плоскости, та к как на торможение влияет но площадь соприкосновения, а физическая природа материала [Гернет М.М., 1973 ; Некрасов А.И., 1950].

Однако, вклинение головы, надлопаточной и ягодичной областей, локтевых суставов в межступенчатые промежутки с изгибом туловища в момент соударений влечет увеличение силы трения и тормозит тело, приводит к уменьшению ускорения свободного перемещения тела по наклонной и горизонтальной поверхностям.

Таким образом, при определенном упрощении параметров падения, установлена физико-математическая зависимость для определения факта предшествующего толчка или удара по месту расположения тела на площадке. Применение полученных результатом, после экспериментальной проверки расчетных данных, позволит на этапе предварительного следствия получить математически обоснованную версию происшествия.