Судебно-медицинские аспекты внешней баллистики дробового оружия

Методы, применяемые экспертами при исследовании повреждений дробью, в значительной степени зависят от экспериментальной и теоретической разработки основных положений внешней баллистики гладкоствольного оружия. Существующие методы определения дистанции выстрела из охотничьего оружия по площади поражения дробью имеют различные недостатки.

Olak установил, что диаметры рассеивания дроби на различных расстояниях выстрела прямо пропорциональны времени прохождения дробинами этих дистанций, т. е. рассеивание дроби и время ее полета связаны отношением t₁/r₁ = t₂/r₂, где t₁ и t₂— время движения дроби до первой и второй преград, a r₁ и r₂— диаметры рассеивания дроби на этих преградах. Исходя из этого, автор предложил определять диаметр рассеивания дроби на любом расстоянии (до 100 м), если экспериментально установлено ее рассеивание на каком-то определенном расстоянии (например 10 м). Значения времени берут из таблицы. Этот метод не получил широкого распространения из-за невозможности произвести прямой расчет дистанции выстрела и ограниченности исходной таблицы значений времени.

Chugh (1970) применил известное дифференциальное уравнение прямолинейного движения снаряда в воздухе (при квадратичном законе сопротивления воздуха) и вывел из этого уравнения формулу зависимости скорости и полета дробины от расстояния выстрела.

υ = υ₀e — ( Kx / pd ),    (1)

где υ — скорость полета в данной точке; υ₀ — начальная скорость; е — основание натуральных логарифмов; х — расстояние выстрела (в м), р — весовая плотность сплава свинца, равная для твердой стандартной дроби 11 000 кг/м³, d — диаметр дробины (в мм), К — показатель сопротивления воздуха, определяемый в данном случае формулой 3/2 * С_хП/2, в которой С_х — безразмерный коэффициент сопротивления воздуха, а П — весовая плотность воздуха у поверхности земли, равная 1,225 кг/м³. По данным аэродинамики (А.П. Мельников, 1961), величина С_х для шарообразного тела, движущегося с околозвуковой скоростью, составляет 0,6—0,8, но для расчетов было взято число 0,65, как наиболее отвечающее данным экспериментов. После подстановки в формулу (1) всех значений констант и произведенных сокращений имеем

υ = υ₀e — ( 0,0542x / d ),    (2)

где d — диаметр дробины (в мм); х — расстояние выстрела (в м).

Следует отметить, что константа 0,0542 (при С_x = 0,65) действительна только на дистанции до 100 м.

Чтобы проверить правильность формулы (2), произвели расчет скорости полета дроби диаметром 2,75, 3 и 4 мм при расстояниях выстрела 5, 10, 15, 20 и 30 м, и полученные результаты сравнивали с эмпирической таблицей скоростей (А.И. Толстопят, 1955). В качестве начальной была принята скорость 400 м/с, так как, по данным того же автора, стандартные патроны с бездымным порохом обеспечивают в среднем именно такую начальную скорость полета дроби, тогда как при выстрелах дымным порохом начальная скорость составляет 350 м/с. Оказалось, что вычисленные по формуле (2) скорости на различных дистанциях отличаются от табличных не более, чем на ±5 м/с.

Предложенная Chugh формула полезна при решении некоторых практических задач. По ней, например, можно определять скорость полета дроби на различных расстояниях в тех случаях, когда требуется выяснить ее поражающее свойство. Однако основное значение формулы (2) заключается в том, что она позволяет исследовать баллистические закономерности рассеивания дроби, имеющие прямое отношение к определению расстояния выстрела.

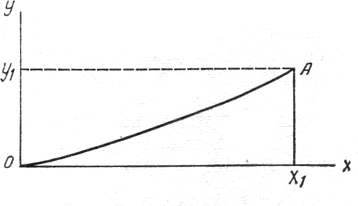
Рис. 1. Теоретическая схема рассеивания дроби. Объяснения даны в тексте.

В настоящей работе авторы поставили целью решить задачу расчета дистанции выстрела по радиусу рассеивания дроби, используя данные внешней баллистики, что дает возможность создать простую и объективную методику вычислений. Схема исследования заключалась в том, чтобы выразить время движения дроби на данное расстояние через радиус рассеивания и затем применить для расчетов уравнение внешней баллистики, выражающее зависимость между временем движения огнестрельного снаряда при прямолинейной траектории и пройденным расстоянием (Б.Н. Окунев, 1943). Чтобы четко сформулировать задачу, рассмотрим на рис. 1 схему движения одной условной крайней дробины, боковое отклонение которой определяет радиус рассеивания. Путь, пройденный дробиной до преграды (линию О А), поместим в прямоугольную систему координат так, чтобы начало системы совпало с дульным срезом ружья, а ось ОХ— с направлением выстрела, и будем рассматривать расстояние выстрела (X) и радиус рассеивания дроби (г) как функции времени (t):

X = f (t) и r = φ (t).

Тогда движение дробины по оси у будет соответствовать ее боковому отклонению (радиусу рассеивания), а расстояние выстрела будет определено отрезком, отложенным по оси X. Поскольку в реальных условиях расстояния ОА и OXi почти одинаковы, то очевидно, что за одно и то же время t дробина пройдет по оси X расстояние, равное ОХ₁, а по оси у — отрезок, равный радиусу рассеивания на данном расстоянии, так как OY₁ = Х₁А.    Следовательно, время прохождения одного сантиметра радиуса крайними дробинами равно отношению t/r. Обозначим эту величину символом Н. Очевидно, что ее значение обратно скорости движения дробин по оси у (если скорость выразить в сантиметрах в секунду). Время t можно определить, зная пройденный путь по оси X, равный отрезку ОХ_и и среднюю скорость движения дроби на этом участке, которая равна υ_сред = (υ₀+υ₁₎ / 2 (υ₁ — скорость в точке х₁).

Тогда время найдем по формуле t = X / υ_сред.

Скорость дроби определяли по формуле (2), а по времени и радиусу рассеивания вычисляли величину Н. Для получения числовых значений этой величины произвели математическую обработку результатов 490 экспериментальных выстрелов из числа опытов, проводившихся А.Ф. Лисицыным (1974) и уже подвергавшихся ранее статистическому исследованию. Эти выстрелы производили из отечественного стендового ружья 12 калибра модели МЦ-8-2 (4-е дульное сужение) сериями одинаковых патронов (от 10 до 100 выстрелов в одной серии) с расстояний 5, 10 и 20 м. С дистанции 10 м произвели 324 выстрела, составившие 13 серий, с дистанций 5 м — 90 выстрелов (8 серий) и с расстояния 20 м — 76 выстрелов (6 серий). Все патроны снаряжали бездымным порохом и различными номерами дроби. В каждой серии опытов определяли средний радиус рассеивания дроби и среднее квадратическое отклонение, в данной работе, кроме этого, вычисляли еще величины: υ_x — скорость движения дроби в точке X; υ_сред — средняя скорость на данном расстоянии; t — время прохождения дробью данного участка пути и Н — время прохождения крайними дробинами 1 см радиуса.

Таблица 1

Результаты математической обработки радиусов рассеивания дроби при экспериментальных выстрелах с расстояния 10 м (V₀= 400 м/с)

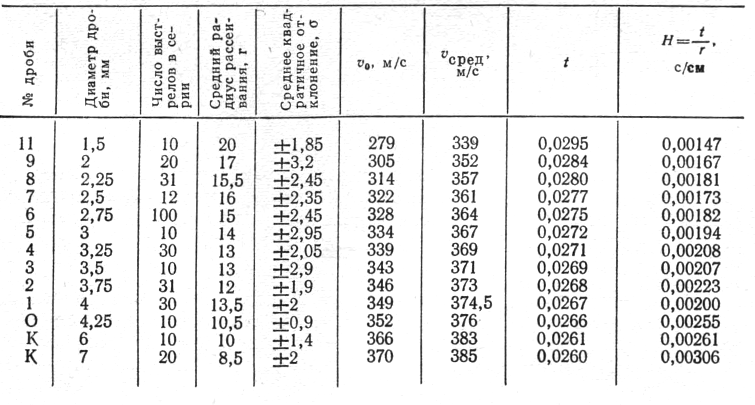
Рассмотрим результаты обработки экспериментальных радиусов рассеивания дроби, полученных при выстрелах с расстояния 10 м.

Из табл. 1 видно, что с увеличением диаметра дроби значения Н (времени прохождения 1 см радиуса рассеивания) возрастают.

Однако для решения поставленной задачи необходимо также выяснить зависимость величины Н от расстояния выстрела. Для этого значения Н вычисляли вышеописанным способом для расстояния выстрелов 5 м (по результатам 90 опытов, составивших 8 серий) и для дистанции 20 м (по результатам 76 опытов, составивших 6 серий). Установлено, что величина Н существенно не зависит от расстояния выстрела, а следовательно, скорость бокового отклонения дробин при различных дистанциях выстрела практически можно считать постоянной.

Этот вывод совпадает с мнением Olak и позволяет использовать величину Н для расчетов дистанции выстрела. Однако предварительно необходимо найти упорядоченное значение этой величины для каждого номера дроби, сгладив небольшие случайные колебания. С этой целью значения Н, указанные в последней графе табл. 1, выравнивали линейной функцией вида H = a₀ + a₁N, где N —условный номер дроби; а_о и a₁ — коэффициенты. В качестве условного первого номера взята дробь № 11 (1,5 мм), а по мере увеличения диаметра на 0,25 мм номер возрастает на единицу. Выравненные значения Н, вычисленные по формуле Н = 0,00147 +0,0000677 N, представлены в табл. 2. При этом путем интерполирования значения Н были получены также для тех номеров дроби, с которыми опыты не производились.

Таблица 2

Выравненные значения величины Н (отношения времени движения дроби к радиусу рассеивания) для стандартных патронов и ружья 12-го калибра с 4-м дульным сужением

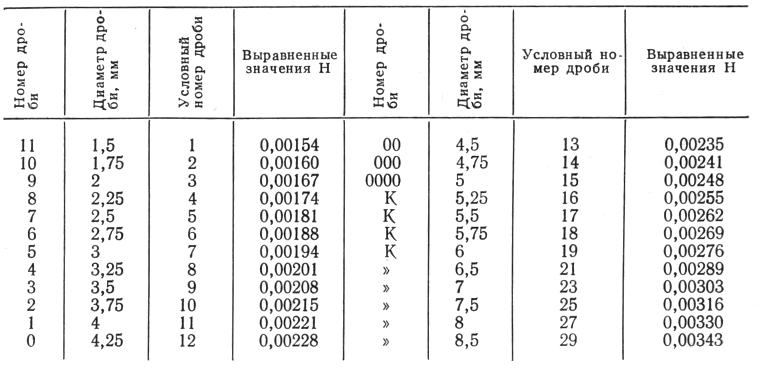
Пользуясь найденными значениями Н, можно приступить к расчету дистанции выстрела. Для этого в каждом конкретном случае по радиусу рассеивания необходимо вычислять величину t, под которой будем понимать время прохождения дробиной радиуса r:

t = H * r,    (3)

а зная время, можно рассчитать длину пройденного пути по оси X (расстояние выстрела), используя уравнение, связывающее время движения огнестрельного снаряда и пройденный путь при прямолинейной траектории (Б.Н. Окунев, 1943). Общий вид этого выражения:

l + bυ₀t = e^bx,    (4)

где υ₀ — начальная скорость дроби; t — время прохождения данного расстояния; X — расстояние выстрела; b —показатель сопротивления воздуха. Из выражения (4) как частный случай можно получить формулу (2), а следовательно, значение b нам уже известно:

b = 0,0542 / d,

где d — диаметр дроби (в мм). Определяя х из уравнения (4) и подставляя вместо b его значение, находим:

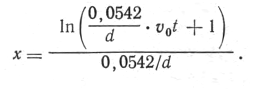
Или, переходя от натуральных логарифмов к десятичным и подставив вместо t произведение Н-r из формулы (3), получим окончательное выражение для расчета дистанции выстрела:

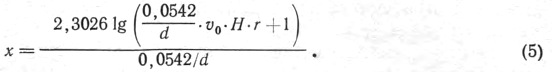
Пример расчета (без предварительной экспериментальной стрельбы): допустим, что площадь поражения дробью имеет размеры 28X33 см и выстрел производился бездымным порохом, дробью № 6 — 2,75 мм — из ствола с 4-м дульным сужением (полный чок). Требуется определить расстояние выстрела. По табл. 3 найдем значение Я для дроби 2,75 мм, которое равно 0,00188. Диаметр рассеивания дроби определим как полусумму двух измерений осыпи (28+32)/2=30 см, а радиус рассеивания здесь равен 15 см. Подставив в формуле значения Н, r и υ₀, имеем:

Таблица 3

Доверительные интервалы к расстояниям выстрела, определяемым по формуле (5)

При сравнении этого результата с данными табл. 1 видно, что в действительности средний исходный радиус рассеивания дроби № 6, равный 15 см, был получен при стрельбе с 10 м.

Но ошибка в 0,2 м, с которой вычислено расстояние выстрела, никакого значения здесь не имеет. Она объясняется тем, что в формулу (5) было подставлено не первоначальное, а выравненное значение величины Я. Гораздо важнее в таких расчетах определить более существенные ошибки, зависящие от широко выраженной вариабельности радиусов рассеивания дроби.

Для расчета таких границ использовали полученные при обработке опытных данных средние квадратичные отклонения радиусов рассеивания дроби для расстояний 5, 10 и 20 м, по которым вычислялись соответствующие ошибки в определении расстояния выстрела. Доверительный интервал 95% для таких ошибок (оптимальный в экспертной практике) был рассчитан по интегральной функции распределения Ре-лея, которому в статистическом отношении подчиняются радиусы рассеивания дроби (А.Ф. Лисицын, 1974). Формула для вычисления 95% интервала после всех преобразований и упрощений имеет вид:

x_1,2 = x ± 1,9 σ_х

где x_1,2 — доверительные границы расстояния выстрела; х — среднее расстояние; σ_х — среднее квадратичное отклонение. Вычисленные по этой формуле доверительные границы представлены в табл. 3. Напомним, что при нормальном законе распределения 95% доверительный интервал равен ±2σ.

Наилучшие результаты предложенный метод дает при условии предварительного проведения экспериментальных выстрелов из того же оружия и теми же патронами. Выстрелы производят строго с расстояния 10 м в количестве не менее 10 в бумажные мишени диаметром около 60 см и более. Вычисляют средний диаметр и радиус рассеивания дроби в серии выстрелов, затем находят по табл. 1 время движения дроби данного номера на расстояние 10 м и делят это число на полученный в результате экспериментов средний радиус рассеивания дроби, устанавливая таким способом величину H для данных конкретных условий стрельбы.

Таблица 4

Эмпирические поправки (индексы) к расчету расстояния выстрела по формуле (5) при различных особенностях оружия и патронов

В тех же случаях, когда эксперименты произвести невозможно, в расчет вводят экспериментальные поправочные индексы, указанные в табл. 4 для основных особенностей оружия и патронов. Индексы вычислены путем сравнения средних радиусов рассеивания дроби, взятых из табл. 1, со средними радиусами, полученными при иных условиях стрельбы (200 опытов), перечисленных в табл. 4.

В расчет вводят поправочный коэффициент М, который определяют перемножая индексы, расположенные в графах А, Б, В, Г (по одному индексу из каждой графы). Например, если выстрел производился из ружья с 4-м дульным сужением (чок) патроном, снаряженным в папковую гильзу бездымным порохом и обычными пыжами, то число М равно 1:

М=1∙1∙1∙1 = 1.

При расчетах по формуле (5) коэффициент М умножают на число H.

Приведем пример: допустим, что на преграде имеется площадь поражения диаметром 35 см и известно, что выстрел производили из ружья с 4-м дульным сужением патроном, который снаряжен дробью № 5 (3 мм) и бездымным порохом в папковую гильзу с применением полиэтиленового пыжа — контейнера. Число М здесь равно:

M=1∙1∙l,3∙1 = 1,3.

Найдем по.табл. 3 значение Н для дроби № 5 (0,00194) и определим по формуле (5) расстояние выстрела:

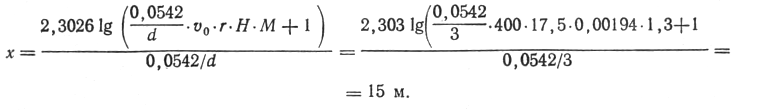
По табл. 4 находим доверительный интервал, который равен ±4 м, т. е. выстрел произведен с расстояния в пределах 11—19 м. С некоторым приближением можно принять, что среднее расстояние выстрела является в то же время и наиболее вероятным.

График зависимости радиусов рассеивания дроби от расстояний выстрела с доверительным интервалом представлен на рис. 2.

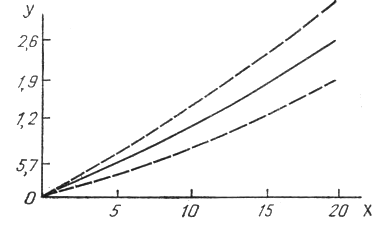
Рис. 2 График аналитической зависимости радиусов рассеивания дроби от расстояния выстрела с 95% доверительным интервалом. По оси абсцисс — расстояния выстрелов (в м); по оси ординат — радиусы рассеивания (в см).

Для вычисления необходимо иметь школьную таблицу десятичных логарифмов.

Данный метод обладает рядом преимуществ. Он основан на точных баллистических закономерностях, учитывает особенности оружия и патронов, легко сочетается с экспериментальной стрельбой в каждом конкретном случае, не требует много времени (около 10 мин), позволяет определить расстояние выстрела в более узких пределах и устанавливать однозначно наиболее вероятную дистанцию выстрела.