Использование трехмерного и математического моделирования для проведения ситуационной экспертизы

Спортивные и специальные профессиональные навыки, которым люди обучились в ходе тренировок, могут быть использованы для причинения телесных повреждений, которые имеют свои особенности и отличаются от травм, нанесенных неподготовленным человеком.

Дифференцировка механизма образования повреждений возможна только при проведении ситуационной судебно-медицинской экспертизы, которая представляется необходимой при расследовании дел, связанных с причинением вреда здоровью и жизни.

Из материалов уголовного дела: Потерпевший Т. пояснил, что обвиняемый схватил его за одежду в районе груди и перекинул через себя, при этом его ноги оторвались от земли и взлетели выше его головы. После чего он упал, сильно ударившись левым боком. Подозреваемый М. показал, что в ходе ссоры они споткнулись о выступ у входа и оба упали на асфальт лицом друг к другу, при этом потерпевший упал на левый бок, а сам М. - на правый. Согласно заключению судебно-медицинской экспертизы, у потерпевшего имелся перелом шейки левого бедра со смещением, который мог образоваться в результате падения и удара наружной поверхностью бедра, что расценивается как средней тяжести вред здоровью по признаку его длительного расстройства свыше 21 дня.

Для установления механогенеза образования телесных повреждений был проведен ряд следственных экспериментов с моделированием вариантов падений согласно версиям потерпевшего и обвиняемого, Эксперименты проводились в спортивном зале Академии физкультуры, г. Хабаровска. Согласно комментариям и корректировкам потерпевшего , были выполнены несколько бросков. После проведения ряда броско в потерпевший указал, что бросок похож на тот, который в отношении его применил подозреваемый М. Присутствующий преподаватель кафедры «Теория и методика спортивных единоборств и тяжелой атлетики» пояснил, что такой бросок называется «броском со стойки с поворотом бедра и захватом за отворот одежды в области груди».

Свидетели, которые видели происшествие, указали на один из бросков, как наиболее точно отражающий происшедшее. Этот бросок оказался «броском со стойки с поворотом бедра и захватом за отвороты одежды в области груди».

После корректировок броска проводилась видеосъемка цифровой камерой «Minolta D Image-5», последовательность кадров видеозаписи переведена в графические файлы. Были выделены три динамические фазы — захват с рывком, подсаживание под статиста, рывок его до момента отрыва ног от земли (0,1 с - 1,7 с); статист находится на спине второго до момента прекращения контакта (1,7 с - 2,1 с); вращение вокруг вертикальной оси тела и собственно падение на покрытие (2,2 с

2,5 с). Общая длительность броска составила 2,5 секунды. Первая фаза оказалась самой длительной — 1,7 с, вторая фаза — 0,4–0,5 с, третья фаза 0,4 с.

В аналогичных условиях был проведен ряд следственных экспериментов с обвиняемым. Чтобы продемонстрировать механизм падения, М. совместно со статистом прошли 1 м по полу спортзала, и, споткнувшись о разложенные спортивные маты, оба упали на них, причем М. упал на правый бок, а статист - на левый бок. Выяснилось, что против- пики падают на маты одновременно — подозреваемый—правой, статист левой боковой поверхностью корпуса. При этом статист, моделирующий роль потерпевшего, взаимодействует с покрытием левой боковой и левой задне - боковой поверхностью корпуса. Общая длительность падения составила также 2,5 с. Первая фаза — захват и одновременное движение участников в сторону препятствия (0,1 с - 0,5 с), вторая фаза свободное падение участников эксперимента до момента удара о покрытие. (0,5 с-0,9 с), длительность 0,4–0,5 с, третья фаза - скольжение по покрытию (матам) до полной остановки (1,0 с - 2,4 с), длительность 1,6 с.

При просмотре видеозаписи падания выявлено нехарактерное поведение обоих участников следственного эксперимента, а именно: при падении, «запнувшись», оба участника отталкиваются от поверхности полa и находятся вне контакта с покрытием (матов) 0,4 секунды.

Для сравнительного анализа была построена трехмерная модель падения при спотыкании о преграду. При сравнении механизмов падения показанного в ходе следственного эксперимента обвиняемым и смоделирoванного падения выявлены следующие несоответствия:

• - При неосознанном (основанном на безусловных рефлексах) падении человек не отталкивается от опоры (пола); цель группировки — снижение высоты падения (то есть уменьшение роста и соответственно высоты падения);
• - Пр и падении в ходе следственного эксперимента, показанного обвиняемым, падающие отталкиваются от пола вверх и вперед (с точки зрения физиологии — это подавление безусловного рефлекса корой человека);
• - Не соответствуют точки контакта с поверхностью (в эксперименте на левую боковую поверхность тела, в ходе моделирования - левый локоть и левое колено).

В судебно-медицинской литературе ссылок на повреждение шейки бедра (у здоровых молодых людей) при падении с высоты собственного роста не выявлено (С.А. Кирсанов, О.Л. Ромадовский, Л.А. Щербин, А.В. Маслов, 1972; Л.А. Щербин, В.В. Дербоглав, B.C. Воронцов, Н.Н. Живодеров, 1972; АЛ . Громов, 1979; Г.С. Бачу, 1981; В.Н. Крюков, 1996).

Математическое моделирование травмы

Исходные данные:

• m = 92 кг — масса «потерпевшего», человека получившего травму;
• М = 80 кг  — масса «нападающего»второго человека;
• I — 1,80 м  — рост «потерпевшего»;
• L = 1,73 м  — рост «нападающего» ;
• d = 5 см  — диаметр шейки бедра на уровне повреждения (по исследованию рентгенограммы потерпевшего);
• у = 0,7-0,5 г/мм2  — прочность нажатия (предельное значение нормального напряжения кости) губчатого вещества («Диагностикум механизмов и морфологии переломов при тупой травме скелета» Т.1./ В.И Бахметьев, В.Н. Крюков, В.П. Новоселов и др. - Новосибирск : Наука. Сибирская изд» тельская фирма РАН, 1996. — 166 с.);
• hc = 1,06 м  — расстояние от центра масс «нападающего» до поверхности земли;
• b = 1,02 м  — расстояние от поврежденного сустава ног и потерпевшего до поверхности земли;
• D = 0,28 м  — поперечный размер грудной клетки потерпевшего;
• t1 = 0,1 с  — время рывка тела (анализ видеозаписи броска);
• t2 = 0,2 с - 0,4 с  — время зависания тела (анализ видеозаписи броска);
• t3 = 0,4 с  — время броска (анализ видеозаписи броска);
• ф = 0,005 - 0,007 с  — время удара о твердую поверхность («Биомеханика травмы» А.П. Громов. — М. Медицина, 1979, 275 с.).

Исследованием данного процесса требуется установить:

1. Силу удара, приходящуюся на бедренную кость, в случае броска тела на землю.
2. Силу удара, приходящуюся на бедренную кость, в случае падения тела в результате спотыкания о выступ.
3. Нормальное напряжение в шейке бедренной кости в результате броска тела и его падения.

1. Исследование динамики броска тела через бедро.

Принимается следующая модель броска: В первый период нападающий делает захват тела потерпевшего. В процессе поворота спиной к «потерпевшему» атакующий рывком взваливает его на себя. Во второй фазе перемещения, атакующий резким движением тазом приводит тело потерпевшего в прямолинейное положение, отрывая его ноги от поверхности. Затем в третьей фазе происходит вращение тела и одновременно совершается бросок тела.

Тело потерпевшего при развороте поворачивается приблизительно на девяносто градусов и падает также как прямолинейный стержень. В последней фазе движения тело потерпевшего ударяется о твердую поверхность боком. Удар приходится в область бедра.

В момент соприкосновения тела о твердую поверхность, для определения ударного импульса применяется теорема об изменении количества движения. Учитывая, что удар тела неупругий, запишем основную формулу закона изменения импульса при мгновенных воздействиях:

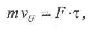
где т - масса падающего тела (в данном случае тела потерпевшего); vu — скорость тела в момент удара, F — ударная сила, подлежащая определению, ф — время удара тела о твердую поверхность. Следовательно, сила удара тела о твердую поверхность определяется по формуле

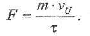
Для определения скорости, с которой тело ударилось о твердую поверхность в результате броска, воспользуемся теоремой об изменении кинетической энергии механической системы. В данной динамической модели движения тела будем учитывать перемещения центра масс тела потерпевшего с момента броска до момента падения на твердую поверхность. То. да имеет место расчетная формула:

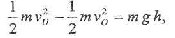(2)

где v - скорость центра масс тела потерпевшего в начале броска через спину противника, h -расстояние от центра масс «нападающего» до поверхности земли; g = 9,81 м/с2 — ускорение свободного падения; т — масса «потерпевшего». Из этой формулы получим выражения для определения скорости тела в момент удара, то есть имеем

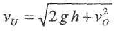(3)

Для определения скорости центра масс тела в момент броска применим метод динамики в инерциальной системе отсчета. Движение тела рассматривается как падение его центра масс с высоты h с начальной скоростью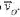 Эта векторная скорость определяется своим модулем vQ и углом б относительно вертикали. На рис. 11 изображена схема падения центра масс тела в системе координат 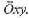S- вертикальная составляющая ударного импульса тела.

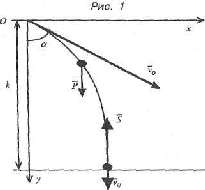
Закон движения центра масс тела в данной координатной системе запишется в виде системы двух уравнений:

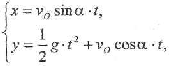(4)

где б - угол направленности броска тела; его среднее значение принимается: б = 45°. В момент удара тела о твердую поверхность второе уравнение системы (4) запишется в виде:

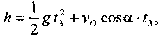(5)

где t3 = 0,4 с - время броска. Из формулы (5) определяется скорость удара; имеем следующую расчетную формулу:

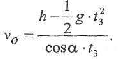(6)

Здесь h = hc + D / 2 = 1,06 + 0,14 = 1,20 м. Подставив в формулу (6) численные значения, получим следующее значение скорости в момент броска:

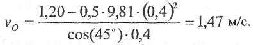
Тогда по формуле вычислим скорость тела в момент удара о твердую поверхность:

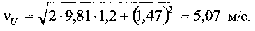
Следовательно, ударная сила вычислится на основе формулы (1):

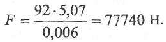
Нормальное напряжение при сжатии кости определяется по формуле:

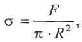(7)

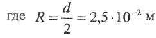- радиус шейки тазобедренной кости на уровне повреждения. Тогда нормальное напряжение в этом случае будет равно:

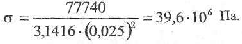
Допустимое, предельное нормальное напряжение [у] для губчатого вещества деформированной кости равно 0,7 - 0,5 кг/мм2; в СИ эта величина будет равна

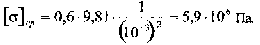
Резюме: Таким образом, сила удара при броске через бедро и падении на твердую поверхность превосходит в 6,7 раза допустимое нормальное напряжение в кости губчатого строения. При такой силе удара неизбежно произойдет деформационная травма кости.

Следует отметить, что в этой динамической модели не учитывалась кинетическая энергия тела при его вращении. Если же учитывать эту энергию, то возрастет скорость в момент удара о поверхности и, следовательно возрастет и ударная сила. Так что в случае броска тела через бедро высчитанное значение ударной силы в действительности несколько выше.

2. Исследование динамики падения тела в результате спотыкания о небольшое препятствие на полу.

В данной модели движение тела потерпевшего также развивается в нескольких фазах. При движении со скоростью V — 3 - 5 км/ч (скорость пешехода) потерпевший спотыкается о выступ высотой 5 см и начинает падать. Это падение рассматривается как вращение тела вокруг оси проходящей перпендикулярно фронтальной поверхности тела через точку выступа. Завершающая фаза движения — боковое падение тела на твердую поверхности, в результате которого удар распределяется по длине всей боковой поверхности тела. На рис. 12. показана схема падения тела.

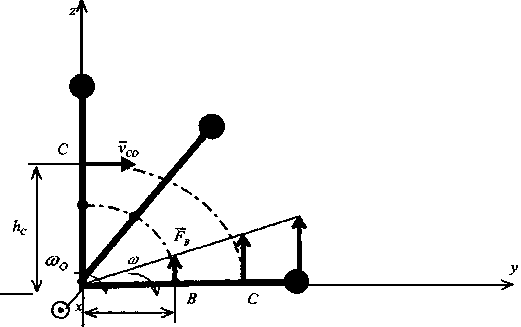
Рис.2

106

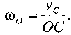
Тело начинает падать с угловой скоростью Примем за

среднее значение начальной скорости центра масс тела vc = 4 км/ч =

1,11 м/с, а ОС = hc - 0,05 = 1,01 м. Тогда начальная угловая скорость

падения тела (как прямолинейного стержня) будет равна:

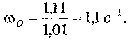
Для определения конечной угловой скорости падения тела на твердую поверхность применим теорему об изменении кинетической энергии. Для рассматриваемого случая она запишется в виде:

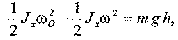(8) где Jх - момент инерции тела относительно оси Ох, проходящей перпендикулярно фронтальной плоскости тела в точке О; h = ОС; щ - угловая скорость тела в момент падения на твердую поверхность.

Тогда из формулы (8) получим

Известен момент инерции тела относительно оси Сх, проходящей через центр масс тела, он равен J =118 кгм2. Тогда по теореме Штейнера-Гюйгенса момент инерции относительно параллельной оси опреде- п ится по формуле

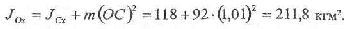
Тогда из формулы (9) определим угловую скорость

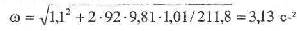
При таком падении тела боком на твердую поверхность ударный импульс распределяется равномерно вдоль всего тела. Таким образом, при определении силы удара в области травмы следует в качестве Массы принять массу бедра ноги, а место приложения ударного им- пульса в этом месте определяется расстоянием b' = 1,02 - 0,05 = 0,97 м — расстояние от поврежденного сустава ноги потерпевшего до поверхно- сти земли; Так как масса бедра составляет 14,2% от всей массы тела,

107

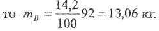
Для определения силы удара F в точке В бедра (в месте травмы сустава) применим теорему об изменения импульса. Она запишется I виде:

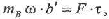
(10)

где ф- время удара бедренной кости о твердую поверхность (она равна ф= 0,006 с) . Тогда эта сила удара будет равна

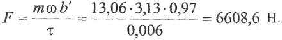
Нормальное напряжение при сжатии кости определяется по фор­муле (7):

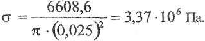
Сравнивая полученное значение нормального напряжения для рассматриваемого случая падения тела с максимально-допустимым напряжением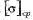 = 5,9 • 106 Па, можно сделать вывод, что такое падение не разрушит шейку сустава.

Заключение:

1. Повреждения на теле Т, наиболее вероятно, образовались при падении в результате применения специального приема (броска со стойки с поворотом бедра и захватом за отворот одежды в области груди) с точкой контакта с твердой поверхностью (асфальт) на левый бок. Вывод основан на соответствии точки первичного контакта и повреждения (данные следственного эксперимента), данных математического моделирования (превышение предельно-допустимой нагрузки на кость в 6,7 раза), что неизбежно приведет к ее повреждению.

2. Повреждения на теле потерпевшего не могли образоваться при обстоятельствах, указанных обвиняемым М. Вывод основан на несоответствии данных следственного эксперимента с данными объемного трехмерного моделирования. Данные математического моделирования - расчетная нагрузка на кость при падении с высоты собственного роста с ускорением или без него, составила 6608,6 Н, что соответствует напряжению 3,37–106 Па, которое мало по сравнению с допустимым нормальным напряжением 5,9×106 Па.